
“Насколько ваша доска ДПК скользкая?”
Скользкость напольного покрытия, использующегося на улице — важный параметр, который необходимо учитывать при выборе материала для террасы, крыльца, ступеней. Особенно это касается напольных покрытий, расположенных под открытым небом, под воздействием дождя и снега. Чтобы всесторонне ответить на вопрос, скользкий декинг ДПК или нет, мы решили провести исследование по определению коэффициента трения скольжения стандартной резиновой обуви (кроссовки) по нашему покрытию, изготовленному из террасных досок марки SAVEWOOD.
Исследование проводилось в лаборатории наполненных полимерных систем нашего стратегического партнера по научно-исследовательской деятельности ИНЭОС РАН, под руководством доктора химических наук, профессора, члена редколлегии журнала “Трение и износ” РАН и НАНБ Краснова А. П., он же любезно согласился дать краткий обзор по вопросу коэффициента трения скольжения для различных материалов.
Теоретическая часть: Трение скольжения
Изучение трения поверхностей твердых тел является чрезвычайно важной задачей. Трение имеет молекулярно-механическую природу. С одной стороны, на площадках непосредственного контакта действуют силы Ван-дер-Ваальса, которые проявляются на расстояниях в десятки раз превышающих межатомное расстояние, и повышаются с ростом температуры. Это взаимодействие объясняет молекулярную составляющую трения. С другой стороны, при движении тел будет происходить внедрение микронеровностей более твердого тела в поверхность менее твердого. Сопротивление деформированию поверхностного слоя обусловило механическую составляющую трения.
Соотношение для силы трения скольжения Fтр=μN, где μ – коэффициент трения скольжения, N – нормальная реакция опоры, носит название закона Амонтона-Кулона. Данный закон справедлив только для определенных нагрузочно-скоростных режимов и сочетаний трущихся материалов. Неожиданным следствием из этого закона является независимость силы трения от формы и размера поверхности номинального контакта тел. Это объясняется тем, что твердые тела контактируют не всей поверхностью, а отдельными пятнами (из-за шероховатости реальных поверхностей). Общая площадь таких пятен очень мала по сравнению с номинальной площадью и растет линейно с увеличением веса тела. В свою очередь, сила трения пропорциональна фактической площади контакта.
Коэффициент трения μ (отношение силы трения к нормальной реакции опоры) может находиться в широком диапазоне значений от примерно 0,001, например, в легко нагруженных подшипниках качения до нескольких десятков для тщательно очищенных одноименных металлов, которые контактируют в вакууме. При трении на воздухе коэффициент трения обычно меняется в пределах от 0,1 до 1.
Коэффициент трения скольжения может быть определен на основе измерения предельного угла наклона плоскости αпред – минимального угла, при котором тело начнет скользить по наклонной плоскости.
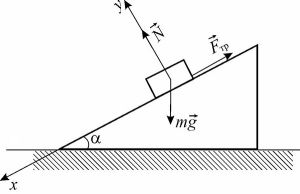
Под действием сил тяжести (mg), трения (Fтр) и нормальной реакции опоры (N) тело может покоиться или скользить по наклонной плоскости (Рис. 1). Если тело находится в состоянии покоя, то
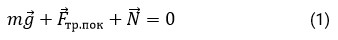
где Fтр. пок – сила трения покоя.
В проекции на ось Х уравнение (1) принимает вид
mgsinα – Fтр. пок=0 (2)
где α – угол при основании наклонной плоскости.
Если изменить угол α при основании наклонной плоскости, то при некотором значении угла αпред тело начнет скользить. При этом сила трения покоя принимает свое максимальное значение, равное силе трения скольжения
Fтр. пок. max = Fтр. ск
В свою очередь, модуль силы трения скольжения определяется выражением Fтр. ск=μN, где μ – коэффициент трения скольжения, а N – сила нормальной реакции опоры.
Скольжение тела в соответствии с вторым законом Ньютона описывается уравнением

которое в проекции на ось Y (рис.1) представляется соотношением 0=N – mgcosα. В результате выражение для модуля силы трения скольжения принимает вид:
Fтр. ск = μmgcosα (4).
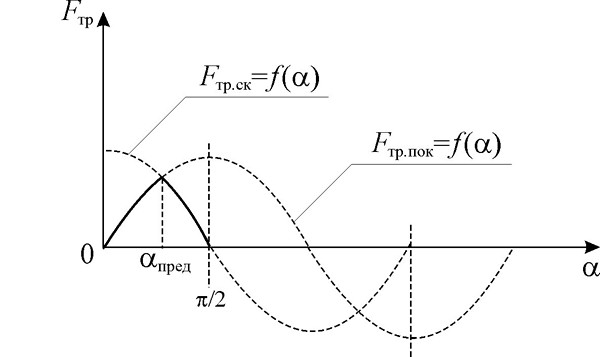
На рис. 2 представлена зависимость силы трения покоя Fтр.пок и силы трения скольжения Fтр.ск от угла α при основании наклонной плоскости. При 0˂α˂αпред на тело действует сила трения покоя, определяемая законом синуса в соответствии с выражением (2). При α=αпред начинается скольжение тела. При этом на него начинает действовать сила трения скольжения, определяемая в соответствии с выражением (4) законом косинуса. При α=αпред силы трения становятся равными:
Fтр.пок = Fтр.ск
или
mgsinαпред = μmgcosαпред
Отсюда получаем связь между углом αпред и коэффициентом трения скольжения
μ = tgαпред,
где αпред – угол наклона плоскости, при котором начинается движение тела.
Экспериментальная часть: определение скользкости покрытия (коэффициента трения скольжения) террасной доски компании Savewood.
Испытание проводилось в соответствии с ГОСТ Р 55908-2013 «Полы. Метод оценки скользкости покрытия».
Наименование материала — Террасная доска (декинг) из ДПК на основе ПВХ с текстурой дерева.
Целью работы являлось определение коэффициента трения скольжения резиновой подошвы по террасной доске, оценка скользкости по СП 29.13330.2011 и сравнение с нормативными показателями, при которых обеспечивается безопасность передвижения людей по покрытию террасной доски.
Испытания проводили:
- при движении по сухой поверхности террасной доски в обуви,
- при движении по влажной поверхности террасной доски в обуви.
В качестве покрытия пола использовали представленные образцы террасной доски на основе ПВХ с текстурой дерева марки SW Fagus производства компании SAVEWOOD. Скорость наклона изготовленного стенда с опытными образцами составляла не более 10 град/мин.
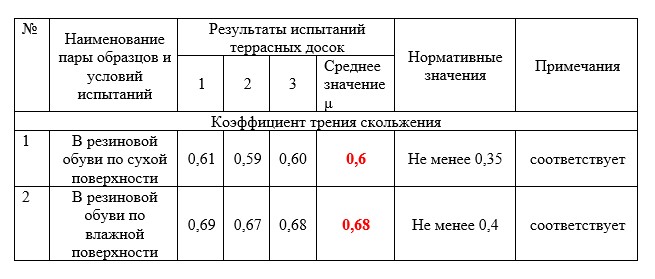
Результаты испытаний представлены в табл. 1.
Нормативные значения коэффициента трения скольжения приняты по СП 29.13330.2011:
– не менее 0,35 в обуви по сухим покрытиям, – не менее 0,4 в обуви по влажным покрытиям.
Вывод:
Террасные доски из ДПК на основе ПВХ с текстурой дерева производства компании Savewood являются безопасными для передвижения людей в обуви, как по сухим, так и по влажным поверхностям.
Для сравнения мы приводим коэффициенты трения покоя и скольжения для пар наиболее распространенных материалов. Эти данные были взяты из справочного пособия “Коэффициенты трения” (издание второе, переработанное и дополненное, авторы И.В. Крагельский, И.Э. Виноградова, МАШГИЗ, Москва 1962 г.).
|
Комбинация материалов.
|
Коэффициент трения.
|
||
|
Сухие и чистые поверхности
|
Смазанные или жирные поверхности
|
||
| Алмаз | Алмаз | 0.1 | 0.05 – 0.1 |
| Алмаз | Металл | 0.1 – 0.15 | 0.1 |
| Алюминий | Алюминий | 1.05 – 1.35 | 0.3 |
| Алюминиевая бронза | Сталь | 0.45 | – |
| Фосфористая бронза | Сталь | 0.35 | – |
| Алюминий | Низкоуглеродистая (малоуглеродистая) сталь | 0.61
0,47* |
– |
| Бронза | Сталь | – | 0.16 |
| Бронза | Чугун | 0.22* | – |
| Спеченная бронза | Сталь | – | 0.13 |
| Графит | Сталь | 0.1 | 0.1 |
| Графит | Графит (в вакууме) | 0.5 – 0.8 | – |
| Графит | Графит | 0.1 | 0.1 |
| Дуб | Дуб (вдоль волокон) | 0.62,
0.48* |
– |
| Дуб | Дуб (поперек волокон) | 0.54,
0.32* |
0.072* |
| Дерево | Чистое сухое дерево | 0.25 – 0.5 | – |
| Дерево | Влажное дерево | 0.2 | – |
| Дерево | Чистый сухой металл | 0.2 – 0.6 | – |
| Дерево | Влажные металлы | 0.2 | – |
| Дерево | Бетон | 0.62 | – |
| Дерево | Кирпич | 0.6 | – |
| Дерево | Влажный снег | 0.14, 0.1* | – |
| Дерево – вощеное | Сухой снег | 0.04* | – |
| Железо | Железо | 1.0 | 0.15 – 0.20 |
| Латунь | Сталь | 0.35 | 0.19 |
| Латунь | Чугун | 0.3* | – |
| Кадмий | Кадмий | 0.5 | 0.05 |
| Кадмий | Хром | 0.41 | 0.34 |
| Кадмий | Низкоуглеродистая (малоуглеродистая) сталь | 0.46* | – |
| Карбид вольфрама | Сталь | 0.4-0.6 | 0.1 – 0.2 |
| Карбид вольфрама | Карбид вольфрама | 0.2 – 0.25 | 0.12 |
| Карбид вольфрама | Медь | 0.35 | – |
| Карбид вольфрама | Железо | 0.8 | – |
| Кирпич | Дерево | 0.6 | – |
| Кожа | Дуб | 0.61,
052* |
– |
| Кожа | Металл | 0.4 | 0.2 |
| Кожа | Дерево | 0.3 – 0.4 | – |
| Кожа | Чистый металл | 0.6 | – |
| Магний | Магний | 0.6 | 0.08 |
| Свинцовистая медь | Сталь | 0.22 | – |
| Медь | Медь | 1 | 0.08 |
| Медь | Чугун | 1.05,
0.29* |
– |
| Медь | Низкоуглеродистая сталь | 0.53,
0.36* |
0.18* |
| Никель | Никель | 0.7 – 1.1, 0.53* |
0.28,
0.12* |
| Никель | Низкоуглеродистая сталь | 0.64* | 0.18* |
| Нейлон | Нейлон | 0.15 – 0.25 | – |
| Олово | Чугун | 0.32* | – |
| Платина | Платина | 1.2 | 0.25 |
| Плексиглас, оргстекло | Плексиглас, оргстекло | 0.8 | 0.8 |
| Плексиглас, оргстекло | Сталь | 0.4-0.5 | 0.4 – 0.5 |
| Полистирол | Полистирол | 0.5 | 0.5 |
| Полистирол | Сталь | 0.3-0.35 | 0.3 – 0.35 |
| Полиэтилен | Сталь | 0.2 | 0.2 |
| Полистирол | Полистирол | 0.5 | 0.5 |
| Резина | Сухой асфальт | (0.5 – 0.8)* | – |
| Резина | Влажный асфальт | (0.25 – 0.75)* | – |
| Резина | Сухой бетон | (0.6 – 0.85)* | – |
| Резина | Влажный бетон | (0.45 – 0.75)* | – |
| Свинец | Чугун | 0.43* | – |
| Серебро | Серебро | 1.4 | 0.55 |
| Сапфир | Сапфир | 0.2 | 0.2 |
| Сталь | Сталь | 0.8 | 0.16 |
| Стекло | Стекло | 0.9 – 1.0,
0.4* |
0.1 – 0.6, (0.09-0.12)* |
| Стекло | Металл | 0.5 – 0.7 | 0.2 – 0.3 |
| Стекло | Никель | 0.78 | 0.56 |
| Тормозные колодки | Чугун | 0.4 | – |
| Тормозные колодки | Влажный чугун | 0.2 | – |
| Твердое углеродное покрытие (пленка) | Твердое углеродное покрытие (пленка) | 0.16 | 0.12 – 0.14 |
| Твердое углеродное покрытие (пленка) | Сталь | 0.14 | 0.11 – 0.14 |
| Ф-4, ПТФЭ, PTFE, Teflon | Ф-4, ПТФЭ, PTFE, Teflon | 0.04 | 0.04,
0.04* |
| Ф-4, ПТФЭ, PTFE, Teflon | Сталь | 0.04 | 0.04 |
| Ф-4, ПТФЭ, PTFE, Teflon | Ф-4, ПТФЭ, PTFE, Teflon | 0.04 | 0.04 |
| Хром | Хром | 0.41 | 0.34 |
| Чугун | Чугун | 1.1,
0.15* |
0.07* |
| Чугун | Дуб | 0.49* | 0.075* |
| Чугун | Низкоуглеродистая (малоуглеродистая) сталь | 0.4,
0.23* |
0.21,
0.133* |
| Цинк | Чугун | 0.85,
0.21* |
– |
| Цинк | Цинк | 0.6 | 0.04 |
Со звездочкой (*) указаны коэффициенты трения скольжения. Без звездочки – покоя. В целом, трение скольжения никак не выше трения покоя.
Компания SAVEWOOD
выражает благодарность
доктору химических наук, профессору,
члену редколлегии журнала
“Трение и износ” РАН и НАНБ, Краснову А.П.








